使用shapely处理地图数据：

计算区域面积
计算区域时候相交
计算相交面积
地图坐标系转换
区域多边形修正

坐标系转换

百度转高德

1
2
3
4
5
6
7
8
from coordTransform_utils import gcj02_to_bd09
def amap_to_bmap(data):
    """
    高德转为百度
    """    
    baidu_lng,baidu_lat = gcj02_to_bd09(data['longitude'], data['latitude'])

    return baidu_lng, baidu_lat

高德转百度

1
2
3
4
5
6
7
8
from coordTransform_utils import gcj02_to_bd09,bd09_to_gcj02
def bmap_to_amap(data):
    """
    百度转为高德
    """    
    amap_lng,amap_lat = bd09_to_gcj02(data['longitude'], data['latitude'])

    return amap_lng, amap_lat

创建多边形：

以上海市虹口区数据为例。

1
2
3
4
5
6
7
8
df = pd.read_csv("/Users/li/Workspace/github.com/py3-labs/lab057/data/blocks.csv")
df = df.loc[df['district_name'] == '虹口'].reset_index(drop=True).iloc[0]
boards = df['district_board']
print(boards[:100])

from shapely.geometry import Point, Polygon
points = [Point(float(x.split(',')[0]), float(x.split(',')[1])) for x in boards.split(';')]
polygon = Polygon(points)

image.png|700

计算多边形面积

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 创建Polygon
from shapely.geometry import Point, Polygon
from pyproj import Geod
import pyproj
import shapely.ops as ops
from functools import partial

points = [Point(float(x.split(',')[0]), float(x.split(',')[1])) for x in boards.split(';')]
polygon = Polygon(points)

# 第一种计算
print("面积01(单位m^2):",polygon.area)

# 第二种计算
geom_area = ops.transform(
    partial(
        pyproj.transform,
        pyproj.Proj(init='EPSG:4326'),
        pyproj.Proj(
            proj='aea',
            lat_1=polygon.bounds[1],
            lat_2=polygon.bounds[3]
        )
    ),
    polygon)

print("面积02(单位m^2):",geom_area.area)

# 第三种计算
geod = Geod(ellps="WGS84")
polygon = Polygon(points)
area = abs(geod.geometry_area_perimeter(polygon)[0])
print("面积03(单位m^2):",area)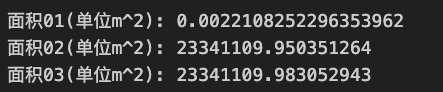

image.png|450

image.png|500

第一种计算方式和后面两种计算方式有这么大差别的原因是：

我们输入的坐标是高德坐标，高德坐标（GCJ-02）是在WGS-84的基础上漂移，因此GCJ-02仍然属于地理坐标系。
shapely默认按照投影坐标系进行计算。
第一种计算方式有问题就是因为，shapely是把经纬度当作投影坐标系来计算（简单地可以认为就是直接坐标系）。
shapely的默认单位是米，那么第一种方式计算出来确实是这样。
第二种计算方式。把坐标从EPSG:4326（可以认为这个就是WGS-84，是一种别称）坐标系转为了aea坐标系。
aea坐标系是一个投影坐标系。也就是通过这个转换，地理坐标系转为了投影坐标系。
在投影坐标系中，经纬度坐标的距离会变成现实中的距离，所以计算面积也就是正确的。
第三种计算方式。是可以处理WGS84坐标系的点，所以也是正确的。
这里需要说明的是，计算距离和面积，需要是投影坐标系。因为这时候投影坐标系可以认为是一个平面，地理坐标系的点不认为是一个平面上。

创建一个半径1公里的圆

既然半径1公里，那么肯定是用在地图中的，那么也就需要转换坐标系。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from functools import partial

import pyproj
from shapely import geometry
from shapely.geometry import Point,Polygon
from shapely.ops import transform

def get_circle(center_lng,center_lat,radius) -> Polygon:
    """
    得到一个圆心多边形,radius单位为米
    """
    local_azimuthal_projection = "+proj=aeqd +R=6371000 +units=m +lat_0={} +lon_0={}".format(
        center_lat, center_lng
    )
    wgs84_to_aeqd = partial(
        pyproj.transform,
        pyproj.Proj("+proj=longlat +datum=WGS84 +no_defs"),
        pyproj.Proj(local_azimuthal_projection),
    )
    aeqd_to_wgs84 = partial(
        pyproj.transform,
        pyproj.Proj(local_azimuthal_projection),
        pyproj.Proj("+proj=longlat +datum=WGS84 +no_defs"),
    )

    center = Point(float(center_lng), float(center_lat))
    point_transformed = transform(wgs84_to_aeqd, center)
    buffer = point_transformed.buffer(radius)
    # Get the polygon with lat lon coordinates
    circle_poly = transform(aeqd_to_wgs84, buffer)
    return circle_poly

这里是在WGS84和aeqd，aeqd和aea一样都是局部的投影坐标系。 aeqd需要给定一个中心点经纬度坐标。所以创建的步骤变为：

创建一个经纬度坐标的Point。这时候还是shapely默认坐标系的，经纬度还没有含意。
把这个坐标通过aeqd->wgs84变换，转为WGS84下的地理坐标系，这时候经纬度有实际意义了。
然后在地理坐标系下，把这个点向外扩大1公里，得到一圈点。
向外扩大这一步可以使用buffer方法，参数就是距离。
然后把这一圈点再通过wgs84->aeqd变化，转为投影坐标系。方便之后的计算（在投影坐标系中计算面积和距离）。

多边形相交

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
poly_block = block_polygon_dict[_block_id]
if poly_block.intersects(poly_circle):    
	# 计算两个Polygon对象的相交面积
	try:
		poly_intersect = poly_block.intersection(poly_circle)

		geod = Geod(ellps="WGS84")
		area = abs(geod.geometry_area_perimeter(poly_intersect)[0])

		is_intersect.append(area)
	except Exception as e:
		print("计算错误",_block_id)
		raise ValueError(e)

在投影坐标系下计算时候相交。
相交区域的面积参考多边形面积计算。

buffer(0)的处理

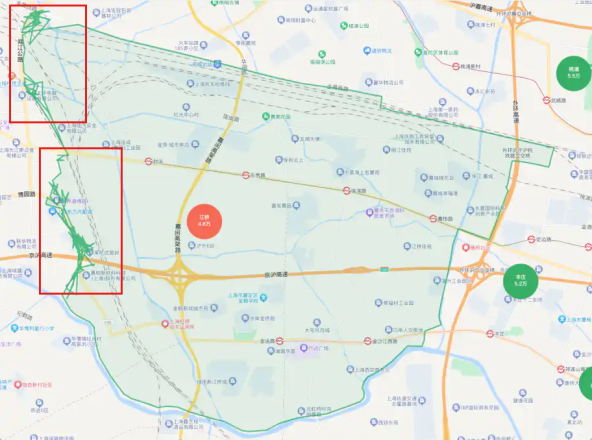
有的时候，我们会遇到区域边界错乱的情况，这个时候可以用buffer(0)来解决，如下图： image.png|500

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
polygon = Polygon([Point(float(x.split(",")[0]),float(x.split(",")[1])) for x in _row["block_board_valid"].split(";")])
if not polygon.is_valid:
	print("not valid",_row['block_id'],_row['block_name'])

	# buffer
	multi_polygon = polygon.buffer(0)
	if isinstance(multi_polygon, Polygon):
		block_polygon_dict[_row['block_id']] = multi_polygon
	elif isinstance(multi_polygon, MultiPolygon):
		# 获得multiPolygon中面积最大的polygon
		max_polygon = max(multi_polygon.geoms, key=lambda polygon: polygon.area)
		block_polygon_dict[_row['block_id']] = max_polygon    
else:
	block_polygon_dict[_row['block_id']] = polygon

is_valid先判断多边形时候有效
没有是上图这种情况is_valid就是False，这个时候就可以用buffer(0)，把多边形改为有效的。
但是会出现两种情况，一种是转为了一个有效的多边形。
第二种是分割成多个多边形，遇到这种情况我们就用最大的一块代替原本的多边形。